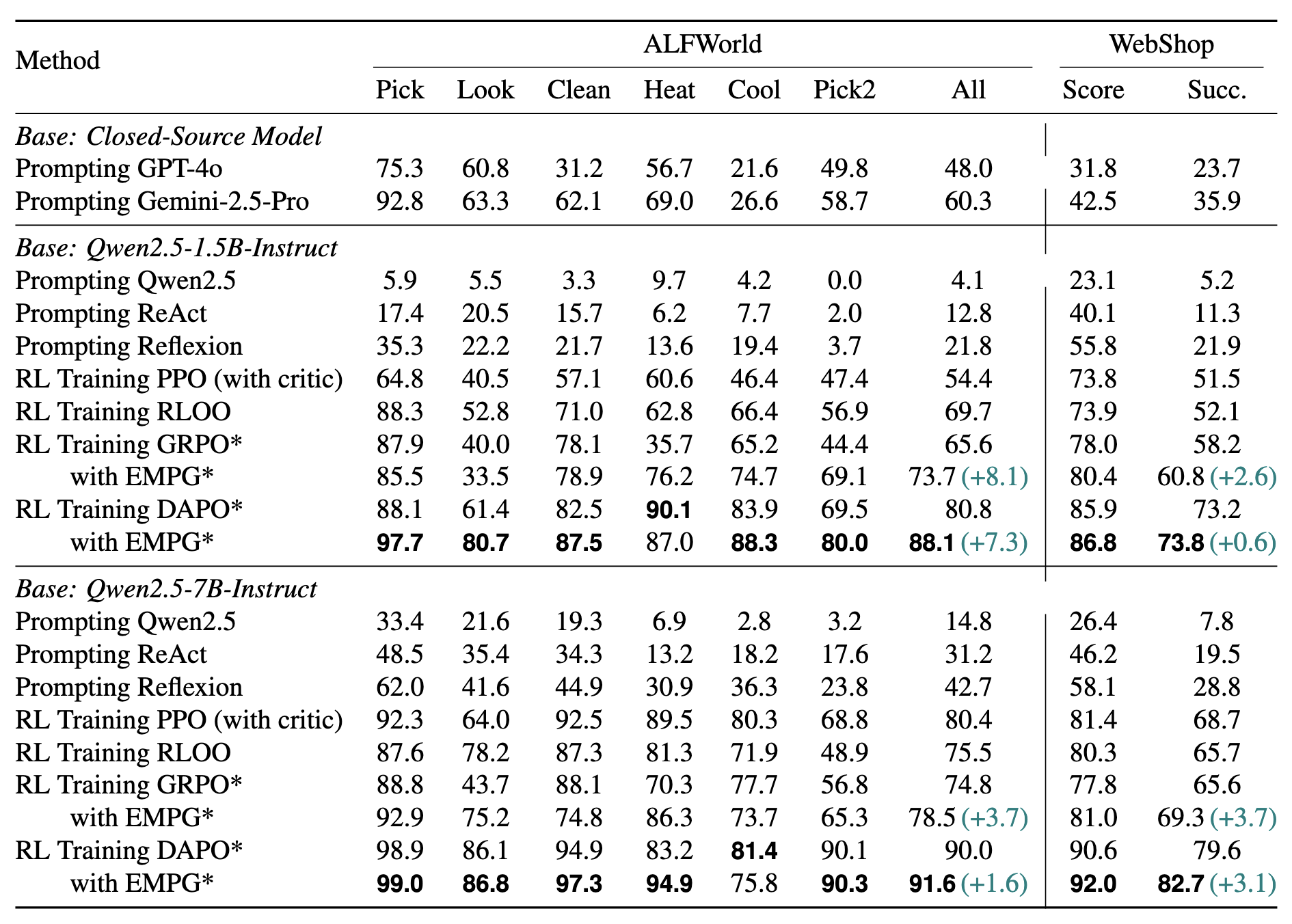
This pseudocode outlines the core logic for calculating the EMPG advantage, demonstrating how to modulate credits based on step-level entropy.
import numpy as np
import torch
def process_token_sequences(
token_id_tensor: torch.Tensor,
start_end_delimiter_seq: list[int],
target_delimiter_seq: list[int],
head_sequence: list[int]
) -> dict:
"""
Processes a token ID tensor to find tokens between specific delimiters and
the end index of a leading sequence.
Args:
token_id_tensor (torch.Tensor): A 1D PyTorch tensor of token IDs.
start_end_delimiter_seq (list[int]): The sequence marking the start and end
of the segments to extract.
For your case, this is [151644, 77091, 1699]
for start, and [151645] for end.
This function assumes the 'start' sequence
is [151644, 77091, 1699] and the 'end' sequence
is [151645] as per your previous requests.
target_delimiter_seq (list[int]): The sequence to mark the end of segments
when found after start_end_delimiter_seq.
For your case, this is [151645].
head_sequence (list[int]): The sequence to find from the beginning of the tensor,
and return its exclusive end index.
For your case, this is [151645, 151644, 872].
Returns:
dict: A dictionary containing:
- 'between_delimiters': A list of tuples, where each tuple contains:
(start_index_of_tokens, end_index_of_tokens, tokens_tensor).
These are the tokens found between `start_end_delimiter_seq`
and `target_delimiter_seq`.
- 'first_head_sequence_end_index': The exclusive end index of the first
`head_sequence` found from the beginning of the tensor.
Returns -1 if not found.
"""
if not isinstance(token_id_tensor, torch.Tensor) or token_id_tensor.ndim != 1:
raise ValueError("token_id_tensor must be a 1D PyTorch tensor.")
if not start_end_delimiter_seq or not target_delimiter_seq or not head_sequence:
raise ValueError("All sequence arguments cannot be empty.")
results = []
start_seq_len = len(start_end_delimiter_seq)
target_seq_len = len(target_delimiter_seq)
head_seq_len = len(head_sequence)
start_seq_tensor = torch.tensor(start_end_delimiter_seq, dtype=token_id_tensor.dtype, device=token_id_tensor.device)
target_seq_tensor = torch.tensor(target_delimiter_seq, dtype=token_id_tensor.dtype, device=token_id_tensor.device)
head_seq_tensor = torch.tensor(head_sequence, dtype=token_id_tensor.dtype, device=token_id_tensor.device)
# --- Part 1: Find the end index of the first head_sequence from the beginning ---
for k in range(len(token_id_tensor) - head_seq_len + 1):
if torch.equal(token_id_tensor[k : k + head_seq_len], head_seq_tensor):
results.append((0, k + head_seq_len))
break # Found the first one, no need to search further
# --- Part 2: Find tokens between start_end_delimiter_seq and target_delimiter_seq ---
for i in range(len(token_id_tensor) - start_seq_len + 1):
if torch.equal(token_id_tensor[i : i + start_seq_len], start_seq_tensor):
for j in range(i + start_seq_len, len(token_id_tensor) - target_seq_len + 1):
if torch.equal(token_id_tensor[j : j + target_seq_len], target_seq_tensor):
tokens_start_idx = i + start_seq_len
tokens_end_idx = j
results.append((tokens_start_idx, tokens_end_idx + 1))
break # Found a pair, move to find the next start_end_delimiter_seq
return results
def compute_empg_advantage(tokenizer, batch, k=1.0, k_f=1.0, zeta=0.1):
"""
Args:
tokenizer: The tokenizer for identifying response segments.
batch: A data batch with 'responses', 'old_entropy', 'advantages'.
k (float): Hyperparameter for self-calibrating gradient scaling.
k_f (float): Hyperparameter for the future clarity bonus.
zeta (float): Hyperparameter for the future clarity bonus.
"""
# --- 1. First Pass: Collect Step-Level Entropies ---
all_step_entropies = []
# segments_to_modify stores {'sample_idx', 'start', 'end'} for each step
segments_to_modify = []
for i in range(batch.batch.batch_size[0]):
# Find "assistant" segments, which correspond to agent steps.
token_segments = process_token_sequences(
batch.batch['responses'][i],
tokenizer.encode("<|im_start|>assistant\n"),
tokenizer.encode('<|im_end|>')
)
for start, end in token_segments:
if start >= end: continue
# Calculate the average token-level entropy for the step
step_entropy = batch.batch['old_entropy'][i][start:end].mean().item()
all_step_entropies.append(step_entropy)
segments_to_modify.append({'sample_idx': i, 'start': start, 'end': end})
if not all_step_entropies: return
# --- 2. Calculate Modulated Advantage Components ---
H = np.array(all_step_entropies)
# Batch-level entropy normalization (Eq. 12) with epsilon = 1e-8
min_H, max_H = np.min(H), np.max(H)
H_norm = (H - min_H) / (max_H - min_H + 1e-8)
# Self-calibrating gradient scaling g(H) (Eq. 10)
g_H_unnormalized = np.exp(-k * H_norm)
mean_g_H = np.mean(g_H_unnormalized)
g_H = g_H_unnormalized / (mean_g_H + 1e-8)
# Future clarity bonus f(H) (Eq. 11)
f_H = np.exp(-k_f * H_norm)
# Convert to tensors for PyTorch operations
g_H = torch.tensor(g_H, device=batch.batch['advantages'].device, dtype=torch.float32)
f_H = torch.tensor(f_H, device=batch.batch['advantages'].device, dtype=torch.float32)
# --- 3. Second Pass: Apply Advantage Modulation (Eq. 8) ---
step_advantages = []
for i, segment in enumerate(segments_to_modify):
idx, start, end = segment['sample_idx'], segment['start'], segment['end']
# Apply self-calibrating gradient scaling
batch.batch['advantages'][idx][start:end] *= g_H[i]
# Add future clarity bonus if there is a next step
next_seg = segments_to_modify[i+1] if i+1 < len(segments_to_modify) else None
if next_seg and next_seg['sample_idx'] == idx:
batch.batch['advantages'][idx][start:end] += zeta * f_H[i+1]
step_advantages.append(batch.batch['advantages'][idx][start])
# --- 4. Final Advantage Normalization (Eq. 7) ---
if step_advantages:
final_adv_mean = torch.mean(torch.stack(step_advantages))
batch.batch['advantages'] -= final_adv_mean